Ableitungsregeln

Information:
Auf dieser Seite präsentieren wir dir die wichtigsten Ableitungsregeln. Diese sind normalerweise auch in einer Formelsammlung zu finden, die du beispielsweise bei der Österreichischen Zentralmatura oder auch bei Schularbeiten verwenden darfst.

Inhaltsverzeichnis:

Ableitung einer Konstanten

Funktion	Ableitung
$ f(x) = C $	$ f'(x) = 0 $

Erklärung:
Die Ableitung von einer Konstanten ist stets Null.

Beispiel:
$ f(x) = 9 \ \ \rightarrow \ \ f'(x) = 0 \\[8pt] f(x) = -3 \ \ \rightarrow \ \ f'(x) = 0 \\[8pt] f(x) = \sqrt{5} \ \ \rightarrow \ \ f'(x) = 0$

Ableitung von Potenzfunktionen

Funktion	Ableitung
$ f(x) = x^a $	$ f'(x) = a \cdot x^{a-1} $

Erklärung:
Wenn du die Ableitung von einer Potenzfunktion bildest, dann schreibst du den Exponenten der Potenzfunktion mit einem Malzeichen vor das x und ziehst anschließend von dem ursprünglichen Exponenten Eins ab.

Beispiel:
$ f(x) = x \ \ \rightarrow \ \ f'(x) = \color{red}{1} \cdot x^{\color{red}{1-1}} = 1 \cdot x^{0} = 1 \\[8pt] f(x) = x^3 \ \ \rightarrow \ \ f'(x) = \color{red}{3} \cdot x^{\color{red}{3-1}} = 3 \cdot x^{2} \\[8pt] f(x) = x^{-5} \ \ \rightarrow \ \ f'(x) = \color{red}{-5} \cdot x^{\color{red}{-5-1}} = -5 \cdot x^{-6} \\[8pt] f(x) = x^{-2} \ \ \rightarrow \ \ f'(x) = \color{red}{-2} \cdot x^{\color{red}{-2-1}} = -2 \cdot x^{-3}$

Faktorregel

Funktion	Ableitung
$ f(x) = c \cdot g(x) $ mit $c \in \mathbb{R}$	$ f'(x) = c \cdot g'(x) $

Erklärung:
Wenn eine Funktion mit einer Konstanten multipliziert wird, dann bleibt bei der Ableitung die Konstante unverändert erhalten.

Beispiel:
$ f(x) = \color{red}{3} \cdot \color{blue}{x^2} \ \ \rightarrow \ \ f'(x) = \color{red}{3} \cdot \color{blue}{2x} = 6x\\[8pt] f(x) = \color{red}{-2} \cdot \color{blue}{sin(x)} \ \ \rightarrow \ \ f'(x) = \color{red}{-2} \cdot \color{blue}{cos(x)} \\[8pt] f(x) = \color{red}{-4.8} \cdot \color{blue}{cos(x)} \ \ \rightarrow \ \ f'(x) = \color{red}{-4.8} \cdot \color{blue}{(-sin(x))} = 4.8 \cdot sin(x) $

(Die Ableitung vom Sinus und Kosinus findest du weiter unten)

Summenregel

Funktion	Ableitung
$ f(x) = g(x) + h(x) $	$ f'(x) = g'(x) + h'(x) $

Erklärung:
Wenn eine Funktion $f$ aus zwei Funktionen $g$ und $h$ besteht, welche durch ein $+$ Zeichen voneinander getrennt sind, dann berechnest du die Ableitung, indem du beide Funktionen einzeln ableitest und die Ergebnisse anschließend addierst.

Beispiel:
$ f(x) = \color{red}{x} + \color{blue}{x^5} \ \ \rightarrow \ \ f'(x) = \color{red}{1} + \color{blue}{5 \cdot x^4} \\[8pt] f(x) = \color{red}{x^{-3}} + \color{blue}{x^2} \ \ \rightarrow \ \ f'(x) = \color{red}{-3 \cdot x^{-4}} + \color{blue}{2 \cdot x^2} \\[8pt] f(x) = \color{red}{sin(x)} + \color{blue}{cos(x)} \ \ \rightarrow \ \ f'(x) = \color{red}{cos(x)} + \color{blue}{-sin(x)} $

(Die Ableitung vom Sinus und Kosinus findest du weiter unten)

Differenzregel

Funktion	Ableitung
$ f(x) = g(x) - h(x) $	$ f'(x) = g'(x) - h'(x) $

Erklärung:
Wenn eine Funktion $f$ aus zwei Funktionen $g$ und $h$ besteht, welche durch ein $-$ Zeichen voneinander getrennt sind, dann berechnest du die Ableitung, indem du beide Funktionen einzeln ableitest und die Ergebnisse anschließend subtrahierst.

Beispiel:
$ f(x) = \color{red}{x^3} - \color{blue}{x^2} \ \ \rightarrow \ \ f'(x) = \color{red}{3 \cdot x^2} - \color{blue}{2 \cdot x} \\[8pt] f(x) = \color{red}{e^x} - \color{blue}{4x^3} \ \ \rightarrow \ \ f'(x) = \color{red}{e^x} - \color{blue}{12 \cdot x^2} \\[8pt] $
(Die Ableitung von der Exonentialfunktion findest du weiter unten)

Produktregel

Funktion	Ableitung
$ f(x) = g(x) \cdot h(x) $	$ f'(x) = g'(x) \cdot h(x) + g(x) \cdot h'(x) $

Erklärung:
Wenn eine Funktion $f$ aus zwei Funktionen $g$ und $h$ besteht, welche durch ein $\cdot$ Zeichen voneinander getrennt sind, dann berechnest du die Ableitung, indem du zuerst die Funktionen $g$ und $h$ einzeln ableitest. Anschließend setzt du in die obige Formel für $f'(x)$ ein. Dies illustriert das folgende Beispiel gut:

Beispiel 1:
$ f(x) = \color{red}{x^7} \cdot \color{blue}{x^{-3}} $. Bestimme $f'(x)$.

Die Funktion $f(x)$ besteht aus den Unterfunktionen $ g(x)=\color{red}{x^7} $ und $ h(x)=\color{blue}{x^{-3}} $. Wenn wir jetzt die beiden Funktionen einzeln ableiten, ergibt sich:

$ g(x) = \color{red}{x^7} \ \ \rightarrow \ \ g'(x) = \color{green}{7 \cdot x^6} \\[4pt]$
$ h(x) = \color{blue}{x^{-3}} \ \ \rightarrow \ \ h'(x) = \color{orange}{-3 \cdot x^{-4}} $

Einsetzen von $\color{green}{g'(x)}$ und $\color{orange}{h'(x)}$ bzw. $\color{red}{g(x)}$ und $\color{blue}{h(x)}$ in die Formel $ f'(x) = \color{green}{g'(x)} \cdot \color{blue}{h(x)} + \color{red}{g(x)} \cdot \color{orange}{h'(x)} $ ergibt:

$ f'(x) = \color{green}{7 \cdot x^6} \cdot \color{blue}{x^{-3}} + \color{red}{x^7} \cdot \color{orange}{(-3) \cdot x^{-4}} $

Vereinfache: $ f'(x) = 7 \cdot x^3 - 3 \cdot x^3 = \underline{ 4 \cdot x^3 } $

Hinweis: Du hättest selbstverständlich auch zuerst die Funktion $ f(x) $ vereinfachen können (zu $f(x)=x^4$) und diese dann entsprechend den Regeln für Potenzfunktionen ableiten können.

---

Beispiel 2:
$ f(x) = \color{red}{sin(x)} \cdot \color{blue}{cos(x)} $. Bestimme $f'(x)$.

Die Funktion $f(x)$ besteht aus den Unterfunktionen $ g(x)=\color{red}{sin(x)} $ und $ h(x)=\color{blue}{cos(x)} $. Wenn wir jetzt die beiden Funktionen einzeln ableiten, ergibt sich:

$ g(x) = \color{red}{sin(x)} \ \ \rightarrow \ \ g'(x) = \color{green}{cos(x)} \\[4pt]$
$ h(x) = \color{blue}{cos(x)} \ \ \rightarrow \ \ h'(x) = \color{orange}{-sin(x)} $

Einsetzen von $\color{green}{g'(x)}$ und $\color{orange}{h'(x)}$ bzw. $\color{red}{g(x)}$ und $\color{blue}{h(x)}$ in die Formel $ f'(x) = \color{green}{g'(x)} \cdot \color{blue}{h(x)} + \color{red}{g(x)} \cdot \color{orange}{h'(x)} $ ergibt:

$ f'(x) = \color{green}{cos(x)} \cdot \color{blue}{cos(x)} + \color{red}{sin(x)} \cdot \color{orange}{(- sin(x))} \\[4pt]$
$ f'(x) = \underline{ cos^2(x)-sin^2(x) } $

Quotientenregel

Funktion	Ableitung
$ f(x) = \dfrac{g(x)}{h(x)} $	$ f'(x) = \dfrac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{h(x)^2} $

Erklärung:
Wenn eine Funktion $f$ aus zwei Funktionen $g$ und $h$ besteht, welche durcheinander dividiert werden, dann berechnest du die Ableitung, indem du zuerst die Funktionen $g$ und $h$ einzeln ableitest. Anschließend setzt du in die obige Formel für $f'(x)$ ein.

Beispiel 1:
$ f(x) = \dfrac{\color{red}{x^5}}{\color{blue}{x^{2}}} $. Bestimme $f'(x)$.

Die Funktion $f(x)$ besteht aus den Unterfunktionen $ g(x)=\color{red}{x^5} $ und $ h(x)=\color{blue}{x^{2}} $. Wenn wir jetzt die beiden Funktionen einzeln ableiten, ergibt sich:

$ g(x) = \color{red}{x^5} \ \ \rightarrow \ \ g'(x) = \color{green}{5 \cdot x^4} \\[4pt]$
$ h(x) = \color{blue}{x^{2}} \ \ \rightarrow \ \ h'(x) = \color{orange}{2 \cdot x} $

Einsetzen von $\color{green}{g'(x)}$ und $\color{orange}{h'(x)}$ bzw. $\color{red}{g(x)}$ und $\color{blue}{h(x)}$ in die Formel $ f'(x) = \dfrac{\color{green}{g'(x)} \cdot \color{blue}{h(x)} - \color{red}{g(x)} \cdot \color{orange}{h'(x)}}{\color{blue}{h(x)}^2} $ ergibt:

$ f'(x) = \dfrac{\color{green}{5 \cdot x^4} \cdot \color{blue}{\color{blue}{x^{2}}} - \color{red}{\color{red}{x^5}} \cdot \color{orange}{\color{orange}{2 \cdot x} }}{\color{blue}{(\color{blue}{x^{2}}})^2} $

Vereinfache:

$ f'(x) = \dfrac{5 \cdot x^6-2 \cdot x^6}{x^4} \\[6pt] f'(x) = \dfrac{3 \cdot x^6}{x^4} \\[6pt] f'(x) = \underline{ 3x^2 }$

Hinweis: Du hättest selbstverständlich auch zuerst die Funktion $ f(x) $ vereinfachen können (zu $f(x)=x^3$) und diese dann entsprechend den Regeln für Potenzfunktionen ableiten können (dies ist auch weitaus sinnvoller!). Um jedoch die Quotientenregel zu verstehen, ist dieses Beispiel sehr gut geeignet.

---

Beispiel 2:
$ f(x) = \dfrac{\color{red}{e^x}}{\color{blue}{x^{3}}} $. Bestimme $f'(x)$.

Die Funktion $f(x)$ besteht aus den Unterfunktionen $ g(x)=\color{red}{e^x} $ und $ h(x)=\color{blue}{x^{3}} $. Wenn wir jetzt die beiden Funktionen einzeln ableiten, ergibt sich:

$ g(x) = \color{red}{e^x} \ \ \rightarrow \ \ g'(x) = \color{green}{e^x} \\[4pt]$
$ h(x) = \color{blue}{x^{3}} \ \ \rightarrow \ \ h'(x) = \color{orange}{3 \cdot x^2} $

Einsetzen von $\color{green}{g'(x)}$ und $\color{orange}{h'(x)}$ bzw. $\color{red}{g(x)}$ und $\color{blue}{h(x)}$ in die Formel $ f'(x) = \dfrac{\color{green}{g'(x)} \cdot \color{blue}{h(x)} - \color{red}{g(x)} \cdot \color{orange}{h'(x)}}{\color{blue}{h(x)}^2} $ ergibt:

$ f'(x) = \dfrac{\color{green}{e^x} \cdot \color{blue}{\color{blue}{x^{3}}} - \color{red}{\color{red}{e^x}} \cdot \color{orange}{\color{orange}{3 \cdot x^2} }}{\color{blue}{(\color{blue}{x^{3}}})^2} $

Vereinfache:

$ f'(x) = \dfrac{e^x \cdot x^3 - 3 \cdot e^x \cdot x^2}{x^6} \\[12pt] f'(x) = \underline{ \dfrac{e^x}{x^3} - \dfrac{3 \cdot e^x}{x^4} }$

Kettenregel

Funktion	Ableitung
$ f(x) = g(h(x)) $	$ f'(x) = g'(h(x)) \cdot h'(x) $

Erklärung:
Wenn eine Funktion $f$ zusammengesetzt bzw. verschachtelt ist, ist die Kettenregel anzuwenden. So ist beispielsweise die Funktion $f(x)=sin(4x)$ verschachtelt, weil $4x$ (und nicht $x$) im Argument des Sinus steht. Dies ist auch bei $f(x)=e^{3x}$, $f(x)=sin(x)^5$ oder auch $f(x)=(6x+1)^4$ der Fall.


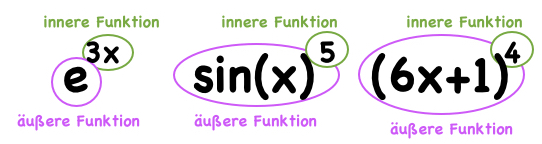Wir merken uns also:
Wenn zwei Funktionen miteinander verkettet sind, ist die Kettenregel anzuwenden.

Diese besagt nun:
Eine verschachtelte Funktion leitest du ab, indem du zuerst die Ableitung der äußeren Funktion berechnest und die innere Funktion unverändert lässt und dann das Ergebnis mit der Ableitung der inneren Funktion multiplizierst.

Um nun die Kettenregel korrekt anzuwenden, bestimmst du zuerst die innere Funktion (hier: $h(x)$) und die äußere Funktion (hier: $g(x)$). Anschließend bildest du die Ableitung von $h(x)$ bzw. $g(x)$ und setzt in die obige Formel ein.



Beispiel 1:
$ f(x) = sin(4x) $. Bestimme $f'(x)$.

Die Funktion $f(x)$ besteht aus der äußeren Funktion $ g(x)=\color{red}{sin(x)} $ und der inneren Funktion $ h(x)=\color{blue}{4x} $. Wenn wir jetzt die beiden Funktionen einzeln ableiten, ergibt sich:

$ g(x) = \color{red}{sin(x)} \ \ \rightarrow \ \ g'(x) = \color{green}{cos(x)} \\[4pt]$
$ h(x) = \color{blue}{4x} \ \ \rightarrow \ \ h'(x) = \color{orange}{4} $

Einsetzen von $\color{green}{g'(x)}$, $\color{blue}{h(x)}$ und $\color{orange}{h'(x)}$ in die Formel $ f'(x) = \color{green}{g'(}\color{blue}{h(x)}\color{green}{)} \cdot \color{orange}{h'(x)} $ ergibt:

$ f'(x) = \underline{ \color{green}{cos(}\color{blue}{4x}\color{green}{)} \cdot \color{orange}{4} } $

---

Beispiel 2:
$ f(x) = e^{3x} $. Bestimme $f'(x)$.

Die Funktion $f(x)$ besteht aus der äußeren Funktion $ g(x)=\color{red}{e^{x}} $ und der inneren Funktion $ h(x)=\color{blue}{3x} $. Wenn wir jetzt die beiden Funktionen einzeln ableiten, ergibt sich:

$ g(x) = \color{red}{e^{x}} \ \ \rightarrow \ \ g'(x) = \color{green}{e^{x}} \\[4pt]$
$ h(x) = \color{blue}{3x} \ \ \rightarrow \ \ h'(x) = \color{orange}{3} $

Einsetzen von $\color{green}{g'(x)}$, $\color{blue}{h(x)}$ und $\color{orange}{h'(x)}$ in die Formel $ f'(x) = \color{green}{g'(}\color{blue}{h(x)}\color{green}{)} \cdot \color{orange}{h'(x)} $ ergibt:

$ f'(x) = \underline{ \color{green}{e^{\color{blue}{3x}}} \cdot \color{orange}{3} } $

---

Beispiel 3:
$ f(x) = (6x+1)^4 $. Bestimme $f'(x)$.

Die Funktion $f(x)$ besteht aus der äußeren Funktion $ g(x)=\color{red}{x^4} $ und der inneren Funktion $ h(x)=\color{blue}{6x+1} $. Wenn wir jetzt die beiden Funktionen einzeln ableiten, ergibt sich:

$ g(x) = \color{red}{x^4} \ \ \rightarrow \ \ g'(x) = \color{green}{4x^3} \\[4pt]$
$ h(x) = \color{blue}{6x+1} \ \ \rightarrow \ \ h'(x) = \color{orange}{6} $

Einsetzen von $\color{green}{g'(x)}$, $\color{blue}{h(x)}$ und $\color{orange}{h'(x)}$ in die Formel $ f'(x) = \color{green}{g'(}\color{blue}{h(x)}\color{green}{)} \cdot \color{orange}{h'(x)} $ ergibt:

$ f'(x) = \color{green}{4 \cdot ({\color{blue}{6x+1}})^3 } \cdot \color{orange}{6} = \underline{24 \cdot (6x+1)^3} $

Ableitung der inversen Funktion

Funktion	Ableitung
$ f(x) $	$ f'(x)=\dfrac{1}{ f^{-1'}(f(x)) } $

Erklärung:
Wenn von einer Funktion die Umkehrfunktion (=inverse Funktion) bekannt ist, so kann es unter Umständen einfacher sein, die Ableitung der ursprünglichen Funktion mithilfe der Ableitung der Umkehrfunktion zu berechnen.

Schritt-für-Schritt:
Du stellst zuerst die Umkehrfunktion $f^{-1}$ auf, die du anschließend ableitest. Dann setzt du in die Formel $ f'(x)=\dfrac{1}{ f^{-1'}(f(x)) } $ ein.

Beispiel:
$ f(x) = \sqrt{x} $. Bestimme $f'(x)$.

Die Umkehrfunktion zu $f(x) = \color{red}{\sqrt{x}} $ lautet $ f^{-1}(x)=x^2 $.
Durch Ableiten erhält man: $\color{purple}{f^{-1'}(x)=2x}$

Einsetzen von $\color{purple}{f^{-1'}(x)}$ und $\color{red}{f(x)}$ in die Formel $ f'(x)=\dfrac{1}{ \color{purple}{f^{-1'}(}\color{red}{f(x)\color{purple}{)}} } $ ergibt:
$ f'(x)=\dfrac{1}{\color{purple}{2 \cdot } \color{red}{ \sqrt{x}}} $

Weitere wichtige Ableitungen von elementaren Funktionen

Funktion	Ableitung
Winkelfunktionen
$ f(x)= sin(x) $	$ f'(x)=cos(x) $
$ f(x)= cos(x) $	$ f'(x)=-sin(x) $
$ f(x)= tan(x) $	$ f'(x)=\dfrac{1}{cos^2(x)} $
Exponentialfunktionen
$ f(x)= a^x $	$ f'(x)=ln(a) \cdot a^x $
$ f(x)= e^x $	$ f'(x)=e^x $
$ f(x)= e^{a \cdot x} $	$ f'(x)=a \cdot e^{a \cdot x} $ (Kettenregel)
Logarithmusfunktionen
$ f(x)= \ _alog(b) $	$ f'(x)=\dfrac{1}{b \cdot ln(a)} $
$ f(x)= ln(x) $	$ f'(x)=\dfrac{1}{x} $
Weitere trigonometrische Funktionen
$ f(x)= sinh(x) $	$ f'(x)=cosh(x) $
$ f(x)= cosh(x) $	$ f'(x)=sinh(x) $
$ f(x)= arcsin(x) $	$ f'(x)=\dfrac{1}{ \sqrt{1-x^2} } $
$ f(x)= arccos(x) $	$ f'(x)=-\dfrac{1}{ \sqrt{1-x^2} } $
$ f(x)= arctan(x) $	$ f'(x)=\dfrac{1}{ x^2+1 } $
$ f(x)= arccot(x) $	$ f'(x)=-\dfrac{1}{ x^2+1 } $